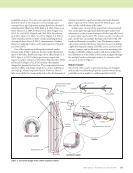
ME TECHNICAL PAPER w modular robotic gripper for tubular components UT. This permits the easier deployment of probes, which is a remarkable advantage in automated inspection. This tech- nique also facilitates the rapid scanning of components with complex geometries and rough surfaces, as described earlier. Traditional EMATs consist of a coil and magnet and are used to generate ultrasonic waves in test metallic samples. The coil is excited by an alternating electric current in the presence of a uniform magnetic field near the surface of an electrically conductive or ferromagnetic material. This alternating Lorentz force plays a major role in transmitting waves (as a source of oscillating stress waves) (ASTM 2017). Depending on the design and orientation of the coils and magnets, different wave modes can be generated in EMAT applications (Kundu 2004). In other words, the orientation, size, and shape of the coil and magnet determine the type of ultrasonic waves and modes required in different inspections. In the following subsection, the authors shall describe in detail the characteristics of the EMATs used in the LTI robot. EMAT Design and Setup In the LTI robot, Lamb waves are generated and received by integrated EMATs to eliminate the need for a point-by-point cross-sectional inspection of tubular components. The main idea behind using Lamb waves in the LTI robot is that as the robot climbs, the network of eight EMATs in the two grippers can communicate and image the entire cross section of the part of the tubular component between the grippers. As a type of guided ultrasound wave, Lamb waves can propagate in plate-like structures. In tubular structures with a small wall thickness-to-diameter ratio, circumferential waves in the tube wall can be considered to be similar to Lamb waves by replacing the cylindrical structure with an equivalent unwrapped plate (Li and Rose 2006 Pierce and Kil 1990). Lamb waves have unique properties that enable sophisticated inspection schemes in general, these waves can propagate over long distances and are more sensitive to discontinuities than traditional bulk ultrasound waves. Thus, the capacity of Lamb waves to inspect the entire cross section of a plate from a long distance makes them a practical choice for the real-time monitoring and inspection of plate-like structures (Rose 2014). Lamb waves are inherently multimodal and dispersive. Therefore, before using Lamb waves to detect discontinuities in pipes, it is necessary to represent their theoretical disper- sion curves to select an effective mode. These curves can be obtained from the governing differential equations and are functions of material properties and sample thickness (Rose 2014). The stainless steel (316L) material used to determine curvature dispersion had an elastic modulus of 200 GPa, Poisson’s ratio of 0.25, a density of 8000 kg/m3, and a thickness of 3.048 mm. A spiral coil (pancake coil) was used to generate omnidirectional Lamb waves to propagate in helical paths and cover the entire cross section of the tube between the two grippers. A permanent magnet generates a static magnetic field, whereas a spiral coil into which 720 M A T E R I A L S E V A L U A T I O N • J U L Y 2 0 2 1 Permanent magnet Spiral coil 12.7 mm N N S S B 0 Figure 5. EMAT components: (a) spiral coil (b) cylindrical magnet and (c) schematic diagram of an EMAT probe. (b) (c) (a) 28.5 mm

J U L Y 2 0 2 1 • M A T E R I A L S E V A L U A T I O N 721 high-frequency excitation current flows generates a dynamic magnetic field and induces an eddy current in the specimens at skin depth. The magnetic field distribution is an important parameter for optimizing the transducer efficiency of an EMAT. Figure 5 shows the spiral coil and cylindrical magnet (12.7 mm diameter and 28.5 mm height) used in this study. The excitation frequency required to excite Lamb waves using a spiral coil was determined using the dispersion curva- ture. For a specific spiral coil, the approximate relationship between the optimal wavelength (!) generated by the spiral coil and spacing of the coil is given by: (1) where OD and ID are the outer and inner diameters of the coil, respectively. For the coil used in this study, the corresponding OD and ID were 12.7 and 0 (zero) mm, respectively. Typically, in an EMAT, a matching condition should be satisfied between the wavelength of the Lamb wave and coil configuration of the spiral coil. The phase velocity and group-velocity dispersion curves corresponding to Lamb waves in a 3.048 mm thick stainless steel structure are shown in Figure 6. When an EMAT is used to generate Lamb waves, the activated modes are selected based on the combination of the periodicity of the transducer and the excitation frequency sent to the trans- ducers. According to the fundamental relation, ! = c/f, the wavelength or period generated by the spiral coil is related to the frequency and phase velocity. The sloped line in Figure 6 represents the activation line at 12.7 mm and the intersecting points of the line with dispersion curves indicate preferential excitation points. There are several ways to select the excita- tion modes for Lamb wave testing. In general, it is preferable to use only the fundamental modes (A0 and S0) and the simplest way is to limit the frequency to a value below the cut- off frequencies in higher modes (such as an excitation frequency in the range of 1 to 600 kHz). As can be observed from the dispersion curvatures, the A0 mode for this spiral coil is highly dispersive. Therefore, S0 was selected for inspection purposes. The red dot in Figure 6 indicates the activation zone when a toneburst excitation with a frequency of #401 kHz was applied to the transducer. Meanwhile, the group velocity of S0 at this frequency was 4924 m/s. Regarding gripper design, the key question is whether or not coils should be formed on the curved surface. Experi- mental tests were conducted, as described in the following section, to answer this question. Experimental Setup To integrate the robotic gripper and EMATs, the first step is to evaluate the effect of tube curvature on the properties of the generated Lamb waves, as sample curvature can signifi- cantly affect the physical properties of the guided waves. In a circular sample, the curvature is defined as the reciprocal of radius as follows: (2) where is the curvature, and r is the radius of the sample. ' = [ OD ID r 1 ¤ = 0 0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10 000 0.5 1 1.5 2 Frequency (Hz) × 106 2.5 3 3.5 4 0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000 0.5 1 1.5 2 Frequency (Hz) × 106 2.5 3 3.5 4 Symmetric S 0, 1, 2, ... Antisymmetric A 0, 1, 2, ... Symmetric S 0, 1, 2, ... Antisymmetric A 0, 1, 2, ... S 0 S 0 A 0 A 0 λ = 12.7 mm Figure 6. Dispersion curves for Lamb wave modes of the 3.048 mm stainless steel plate: (a) phase velocity (b) group velocity. (a) (b) Phase velocity (m/s) Phase velocity (m/s)