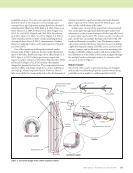
722 M A T E R I A L S E V A L U A T I O N • J U L Y 2 0 2 1 Preliminary tests were conducted to describe the effect of curvature on Lamb wave excitation. Tubes with different diameters (73.025, 88.9, and 114.3 mm) and a plate with an infinite diameter were considered (Figure 7). All samples were made of 316L stainless steel with the same thickness (3.048 mm) to minimize errors in measurement. A data acquisition system was used to generate and receive Lamb waves using the designed EMAT. In all measurements, the EMAT was driven by a five-cycle toneburst with a center frequency of 401 kHz. The waves were excited using the computed burst frequency with an arranged receiver gain of 60 dB. Note that there is also a matching requirement for the receiver and input preamplifier. Depending on the burst frequency, bandpass filtering with a cut-off frequency of 325 to 475 kHz was applied. Results and Discussion In the following sections, two sets of experiments are carried out. First, the EMAT is used to investigate how tube curva- tures influence Lamb waves propagation. Then, the tests are performed in a semiautomatic manner in which the designed gripper was attached to a robotic arm. Effect of Tube Curvature on Lamb Wave Excitation Using EMATs There are two potential configurations for integrating EMATs into the fingers of an LTI robot. In the first configuration, the coils conform with the tube’s surface. This configuration requires a softer design for embedding coils in the pads. In the second configuration, the coils can be placed on the flat surfaces of fingers this does not require embedding the coils into the pads. To investigate the effect of tube curvature on Lamb wave propagation, the samples in Figure 7 were used with two different configurations. First, the coils were fully attached to the magnets. In this case, the coils do not conform with the surface (there is no full contact between the coil and curved surface). This case was called “nonconformed.” Mean- while, in the second condition, the coil was in full contact with the surface (“conformed” case). A schematic of these two cases is shown in Figure 8a with an arbitrary pipe cross section. ME TECHNICAL PAPER w modular robotic gripper for tubular components 3.048 × 304.8 × 609.6 mm 316L stainless steel sheet 316L welded stainless steel pipes OD = 114.3 mm OD = 88.9 mm OD = 73.025 mm (κ = 0.017 mm ) 1 (κ = 0.022 mm ) 1 (κ = 0.027 mm ) 1 Figure 7. Hollow cylinders (pipes) and the plate used in this study. Figure 8. Schematic view of the coil configuration in EMATs testing: (a) nonconformed case (left) and conformed case (right) (b) Lamb wave excitation in pipes with spiral coils and cylindrical magnet (using the conformed configuration). (a) (b) N N Cylindrical magnet Coils Surface

J U L Y 2 0 2 1 • M A T E R I A L S E V A L U A T I O N 723 To achieve an optimal gripper design it is of interest to use similar coils and magnets, especially in terms of geometry and dimensions. Therefore, tests were conducted using a cylin- drical magnet and the coil described in Figure 5. As shown in Figure 8b, the tests were performed with a pitch-catch config- uration (separate but identical transmitter and receiver) to mimic communication between the eight EMATs in the LTI robot. In these tests, no additional normal force was applied to the coils and the magnets were in full contact with the surface to avoid liftoff between the EMAT transducer and substrate. Figure 9 shows the signals received using a cylindrical magnet in the nonconformed and conformed configurations. The signal was recorded when the two EMATs were located 100 mm away from each other. In all cases, the arrival time of the selected Lamb mode could be identified using the group velocity determined from the dispersion curves. For example, the plate signal (Figure 9a) could confidently be identified as the S0 Lamb wave mode due to its correct arrival time at 52 μs. This figure also reveals that the nonconformed coil resulted in slightly higher amplitudes compared to the conformed configuration in all pipe samples. Figure 10a compares the two configuration responses with respect to the curvature of each tested pipe. On an average, the amplitude of the received signal decreased by 9.2% when the coils conformed to the surface. Therefore, it may be stated that the conformed configuration did not improve signal amplitude when compared to the nonconformed configuration under similar test conditions. In the next part, this result is consid- ered in the gripper design for the LTI robot. The time trace in Figure 9 reveals that the waves have different propagation velocities in each specimen. The group velocity in each case can be determined using the arrival time of the received signal from the generated wave pulse (the time of arrival). Figure 10b shows the effects of curvature on the wave propagation velocity. It can be seen in the figure that group velocities in the conformed and nonconformed config- urations were almost consistent, which justifies that the coil conformation does not affect wave velocity. However, sample geometry significantly influences group velocity as shown in Figure 10b, there is an inverse relationship between specimen curvature and group velocity. Based on these tests and the complicated design requirements to embed and conform EMAT coils to the tube surface in the LTI robot, the second configuration was selected (nonconforming case) for tube inspection. 0 0 2 4 –2 –4 20 40 60 Time (μs) 80 100 120 0 0 2 4 –2 –4 20 40 60 Time (μs) 80 100 120 Nonconformed coil Conformed coil 0 0 2 4 –2 –4 20 40 60 Time (μs) 80 100 120 Nonconformed coil Conformed coil 0 0 2 4 –2 –4 20 40 60 Time (μs) 80 100 120 Nonconformed coil Conformed coil Figure 9. Lamb wave signals with spiral coils in nonconformed and conformed configurations: (a) single signal in plate (b) 73.025 mm OD pipe (c) 88.9 mm OD pipe and (d) 114.3 mm OD pipe. (a) (b) (c) (d) 16 1.5 2 2.5 3 3.5 4 4.5 18 20 22 κ (1/m) 24 26 28 15 3800 4000 4200 4400 4600 4800 5000 5200 5400 20 κ (1/m) 25 30 Nonconformed Conformed Nonconformed Conformed Figure 10. Effect of curvature on the wave propagation in materials with different diameters curvature versus: (a) maximum amplitude (b) group velocity. (a) (b) Amplitude (V) ×104 Amplitude (V) ×104 Amplitude (V) ×104 Amplitude (V) ×104 Maximum amplitude (V) ×104 Group velocity (m/s)