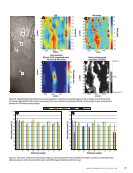
Results and Discussion
The results indicate that using only two TDOAs, obtained
by positioning the robotic arm at two points on the grid, the
leakage direction and distance can be estimated with an
error of less than 1° and 40 mm, respectively. Figure 4 illus-
trates the minimum achievable error when each grid point is
paired with other points. One can clearly notice that not all
combinations result in 40 mm distance accuracy, highlight-
ing the importance of systematically selecting the second
point for the second TDOA for distance estimation. Figure 4
explores this concept further by examining the combinations
when points 1 and 29 are used as the initial measurement
points. While most combinations yield good accuracy, there
are certain points that the robot should avoid as the second
measurement location to maintain high accuracy. Figure 5
provides color maps of the grid, where the white square indi-
cates the first measurement point, representing the robot’s
initial position. By accessing the error distribution for each
grid point, the robot can strategically choose the second mea-
surement point to minimize estimation error.
Analysis of Figure 5 reveals that, in most cases, moving ver-
tically is not a wise choice, and horizontal movement is gen-
erally more effective. This is because vertical movement often
fails to provide additional information for solving the hyper-
bolic equations due to insufficient change of TDOA, as indi-
cated in Figures 5c and 5d. This leads to substantial errors in
source localization, as the two resulting hyperbolas tend to be
nearly parallel, reducing the accuracy of the estimation.
Access to maps like those in Figure 5 can significantly aid
the agent in decision-making to obtain the second TDOA.
However, in real-world scenarios or with larger grids, con-
structing these maps and providing the agent with access
becomes challenging. Therefore, we explored the range of
errors the agent might encounter if it selects points randomly.
As discussed earlier, relying on only two points on the grid
and choosing the second location randomly is not an effec-
tive solution. Generally, increasing the number of points
improves source localization accuracy. The key question
is how many points the agent should randomly select to
achieve reliable accuracy. To investigate this, for each fixed
first location, we randomly selected two additional points 100
0
0
0.2
0.4
0.6
10 20 30
Second data collection point
40 50 60 70
0
0
0.2
0.1
10 20 30
Second data collection point
40 50 60 70
0
0
0.2
0.4
0.6
10 20 30
Initial measurement point
40 50 60
0
0.2
0.4
0.6
0.8
1.0
10 20 30
Initial measurement point
40 50 60
Figure 4. Minimum achievable error for each point in combination with subsequent points: (a) error in distance estimation (b) error in direction
estimation. Error distribution in leak distance estimation: Analysis based on fixing the first measurement point and its combinations with
subsequent points: (c) Point 1 (d) Point 29.
A P R I L 2 0 2 5 • M AT E R I A L S E V A L U AT I O N 55
Error
(m)
Error
(m)
Error
(m)
Error
(m)

times, estimated the source location, and averaged the error in
distance over these 100 trials. This approach provides a solid
foundation for understanding the expected error range when
the agent has data from only three locations. The same meth-
odology was applied for scenarios with six, eight, and ten
randomly chosen locations. Figure 6 illustrates the expected
error an agent might encounter when starting from differ-
ent grid points and selecting subsequent points at random.
The expected error is significantly higher in some cases,
primarily due to the agent’s potential vertical movement,
which increases the error. Although the expected error range
becomes narrower when the number of points is increased
to 10, the robot still expects a 120 mm to 140 mm error in
distance.
An alternative approach involves providing the agent
with additional information to enable more strategic
motion planning. This additional information is obtained
by rotating the microphone about the Z-axis. Figure 7 illus-
trates how the TDOA and amplitude change as the micro-
phones rotate. As expected, the TDOA reaches zero when
the robot is oriented directly toward the sound source
(leakage). While one may expect to receive the maximum
amplitude once the microphones are directed toward the
leakage source, our analysis shows that the maximum
amplitude slightly deviated from that direction, as depicted
in Figure 7b. Consequently, starting from an initial position,
the robot can rotate about the Z-axis to accurately deter-
mine the direction of the sound source (leakage) when the
TDOA reaches zero. Once the direction is established, and
knowing that horizontal movement is more effective, the
robot can then move laterally to capture a second TDOA
reading and localize the sound location. This movement
strategy is tested using our robotic dog platform to replicate
more realistic scenarios.
ME
|
LEAKLOCALIZATION
1 0.25
0.2
0.15
0.1
0.05
2
3
4
5
6
7
8
–600
–800
–1000
–1200
–1400
X (mm)
–1600
–1800
–2000
–250 –200 –150 –100 –50 0 50 100
–600
–800
–1000
–1200
–1400
X (mm)
–1600
–1800
–2000
–250 –200 –150 –100 –50 0 50 100
8 7 6 5
X
4 3 2 1
1
0.2
0.3
0.4
0.5
0.6
0.1
2
3
4
5
6
7
8
8 7 6 5
X
4 3 2 1
19.722
5
– 14.5775
14.5775
14.5–
77 5
– 14.5775
–
19.7225 19.7225
– 19.722
5
– 19.722
5 19.722 5
– 19.722
5
–
5
–
5
–
5
5
–19.722518.007
Leakage Leakage
Figure 5. Distribution of error in the grid with the first location at (a) Point 1 and (b) Point 29. Intersection of hyperbolas constituted from points (c)
1 and 2, and (d) 1 and 9.
0.18
0.17
0.16
0.15
0.14
0.13
0.12
0.11
0.1
0.09 0 10 20 30 40 50 60 70
Location index
3 random points
6 random points
8 random points
10 random points
Figure 6. Expected error when the first position is fixed, and
subsequent points are chosen randomly.
56
M AT E R I A L S E V A L U AT I O N • A P R I L 2 0 2 5
Y
(mm)
Y
(mm)
Y Y
Expected
error
(m)
Error
(m)
Error
(m)