to calculate temperature. The lamp is current controlled by a programmable DC power supply. The lamp had been cali- brated using a NIST-traceable transfer pyrometer (Gibson et al. 1998) to achieve predetermined temperature set points when powered at a specific current, shown in Table 1. The tempera- ture is set to each set point and allowed to stabilize for 1 min, starting from 1300 °C. An oscilloscope is used to monitor both of the sensor voltages to ensure that they remain within the acceptable range. The aperture is set such that the higher sensor is reading 85 of its saturation voltage when the cali- bration source is set to 2300 °C, ensuring that the sensors will not saturate. At each temperature set point, 5 s of the photodetector signal is recorded at 200 kHz. The temperature is increased to each progressively higher set point and stabilized for 1 min before a 5 s data capture. The amperage set points for each temperature are shown in Table 1. A flowchart of the calibration measurement process is shown in Figure 3. Calibration Calculations Because both detector channels are acquired synchronously, each element corresponds to measurement at the same point in time. For each temperature set point Ti, the ratio, S1(T)/ S2(T), is calculated by elementwise division of the timeseries high and low wavelength photodetector signals after dark current subtraction, Ri(t) = S1(t)/S2(t). The median value of the time series ratio Ri(t) is recorded for each temperature set point and used to regress to values of A and B in Equation 7, which follows from Equation 6: (7) T i = A ln$ B Ri ! " # % Within each 5 s data capture of Ri(t), the standard devi- ation of the temporally middle 400 values was calculated to identify trends in signal variation as a function of temperature. Assuming a constant random distribution of noise, ˜, in the otherwise constant sensor signals S1(T) and S2(T) at a constant temperature, the noise is proportionally larger, relative to the signal. As a result, the variance in the ratio S(λ1,T) + ˜/S(λ2,T) + ˜ should increase with decreasing temperature, which decreases with sensor signal. Spatial Normalization Calculations There are many effects that may change the ratio of high and low wavelength signals spatially over the build plate, includ- ing but not limited to path length variation, angle-dependent transmission through the optics, and spherical aberration. It can be argued that the variation can be described as a proportional change in transmission in each high and low wavelength separately, which varies as a function of position and not in time. To quantify the proportional reduction in transmission, it is assumed that temperature, and therefore the ratio of low/high wavelength signals, is a constant across the build plate. Full build plates are fabricated once the process has reached a steady state, four layers are recorded. The raw data for the high and low signals from each of these layers is rastered into 50 μm resolution images. For each layer, the low wavelength signal image is elementwise divided by the high wavelength signal image, to produce a single ratio signal image. The four ratio images are averaged. The averaged image Center the laser focus on the center of the build plate Drop build plate by 45 mm, then place box in the center of it Record data with the bulb off Let stabilize for 1 min Prepare a data set Process one layer and set the detector gains Turn lamp to next set point Record data Figure 3. Flowchart of the calibration measurement process. T A B L E 1 Representative temperature and current set points used for calibration Temperature (°C) 1300 1400 1500 1600 1700 1800 1900 2000 2100 2200 2300 Current (A) 7.08 7.61 8.21 8.9 9.64 10.44 11.27 12.18 13.13 14.11 15.14 A P R I L 2 0 2 2 • M A T E R I A L S E V A L U A T I O N 67

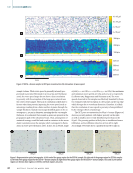
is then normalized such that the average value in the center 2 × 2 mm square on the build plate is equal to one. This image contains all of the values used for correcting the incoming tem- perature data. For every raw temporal datum, the nearest pixel in the correction value image was located, and the raw ratio datum’s value was divided by that correction value, producing a corrected ratio which was used to calculate the spatially corrected temperature. Results and Discussion The data are fit to the regression formula derived from Planck’s law, and temporal and spatial variation from the sensor is characterized. Comparison is made against in situ application of Wein’s displacement law, an alternative method of calculat- ing temperature. Regression and Variation Prior to standardization, the lamp was powered on to 1700 °C from room temperature. The signal from the low wave- length photodetector was measured over time as power was applied to the lamp to determine the timescale required to reach steady-state temperature. The results of signal versus time are shown in Figure 3. It was determined that steady state was achieved within 2 s. The 1 min dwell time for tem- perature to stabilize is significantly more than required. After this measurement is taken, the lamp is powered off until it is no longer visibly emitting light before proceeding with the standardization. Regressing the median value of Ri(t) (over the central 400 points) for each temperature against the set points yields an equation of A = 618.75 and B = 0.681, with an R2 value of 0.996, as shown in Figure 4. The model estimates the setpoints with a root mean square error (RMSE) of 19.42 °C. For each of the 400 temporally middle values of Ri(t) at each temperature set point, the temperature T(t) was calcu- lated based on the calibration regression model developed in Equation 7. The standard deviation of these 400 tempera- ture values was recorded to quantify sensor noise in terms of measured temperature. These standard deviations are shown in Table 2 and plotted as error bars in Figure 4. As expected, the standard deviation of the data collected increases with decreasing temperature, as the temperature is calculated from a ratio of two signals, which both contain noise. As the signals decrease with decreasing temperature, the noise makes up a larger portion of the ratio’s variance. Measured temperature standard deviation as a function of temperature set point is shown in Table 2. It is important to note that the standard deviation of the sampled data is not a good metric of sensor uncertainty. Because anomalous signals span more than one temporal data sample (5 μs), the uncertainty of the dual photodiode sensor is a function of the length of time that the signal is acquired. The equation to calculate standard error, SE = σ/√n, can be rear- ranged to calculate the number of samples required to reduce the standard error below a defined threshold value of SE: (8) n = ceiling ! #2 , % &"SE$ ) )* ’ ( + + The results of applying this formula to various values can be found in Table 3. To achieve the same standard error as 2300 °C but at other set point temperatures, the required sampling time roughly doubles at 2000 °C and is roughly 100× as high at 1300 °C. Here, standard error is a qualitative descriptor of how difficult it is to differentiate two signals. For example, to detect a process deviation in a signal at 1300 °C will take roughly 100× as long as detecting a process deviation of similar magnitude in a signal at 2300 °C. This illustrates that the quickest process deviation that can be resolved by this dual-photodetector method is a function of the temperature of the signal’s source. It should be noted that while the photodetectors have inherent noise, these standard deviations are a function of the 0.00 0.25 0.50 0.75 1.00 1.25 1.50 1.75 2.00 0.25 0.20 0.15 0.10 0.05 0.00 Seconds after powered on Figure 4. Low sensor voltage versus time when lamp is powered on. Due to the small thermal inertia of the lamp, a steady-state temperature is reached within seconds. T A B L E 2 Regression prediction and data standard deviation by set point Set point (°C) 1300 1400 1500 1600 1700 1800 1900 2000 2100 2200 2300 Standard deviation (°C) 734 382 225 190 148 130 109 104 87.8 77.5 73.0 Model prediction (°C) 1295 1361 1547 1603 1688 1803 1915 1998 2090 2206 2290 ME | MELTPOOLMONITORING 68 M A T E R I A L S E V A L U A T I O N • A P R I L 2 0 2 2 Low sensor voltage