The inverse effect also applies whereby an ultrasound wave
forces the charged particles (electrons) to move, which, under
a bias magnetic field, produce eddy currents under the surface
of a conductive specimen with a density as described by Isla
and Cegla (2016): ​ ​ ​
(2)​ ​ J​e​​ =σ(​​v ​ × ​ BO​​​)​​​​​
where ​
σ​ is the conductivity of the material, and ​
v​ is the velocity of the charged particles.
These eddy currents are then inductively picked up by the
coil of the EMAT. The Lorentz force is linear in Je and BO, and the
maximum force in a given direction n is obtained when the three
vectors (n, Je, and BO) are mutually perpendicular (Ribichini et
al. 2011). These factors must be considered when designing the
optimal geometry for periodic permanent magnet (PPM) EMATs.
Similarly, magnetostriction is a property of ferromagnetic
materials that causes them to change shape or dimension
when exposed to a magnetic field. The term “magnetostric-
tion” is derived from “magneto,” which refers to magnetism,
and “striction,” which means a change in shape or size. This
effect allows magnetostrictive materials to convert electromag-
netic energy into mechanical energy and vice versa, a conver-
sion that is analogous to the piezoelectricity principle. When
a ferromagnetic material is subjected to a magnetic field, the
alignment of its magnetic domains changes, resulting in a
rearrangement of the atomic or molecular structure. This rear-
rangement causes the material to either expand or contract,
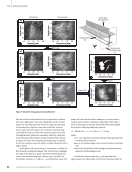
thereby changing the material’s overall dimensions, as shown
in Figure 2. The effect is reversible, meaning the material will
return to its original shape when the magnetic field is removed.
The dimensional change of the material causes strain, also
referred to as the Joule effect (Joule 1847), whereas the reverse
phenomenon is referred to as the Villari effect (Villari 1865).
Magnetostrictive materials with large magnetostriction
coefficients, such as Terfenol-D (an iron–terbium–dysprosium
alloy), Hyperco 50A alloy (an iron–cobalt–vanadium soft
magnetic alloy), Galfenol, or Remendur, have been widely
used as magnetostrictive patches to generate and receive ultra-
sound in different applications (Kim and Kwon 2015 Sha and
Lissenden 2021 Vinogradov et al. 2017). The work reported in
this paper focuses on discovering and testing a novel magneto-
strictive EMAT sensor, including a presentation of the founda-
tion behind magnetostrictive EMAT.
Like Lorentz-force EMATs, magnetostrictive patch sensors
require a magnetic bias to impose a static magnetic field in the
magnetostrictive patch and a coil with an excitation current to
generate a dynamic magnetic field (perturbation) in the patch.
The relative orientation of the static magnetic field and the
magnetic perturbation determine the mode of the generated or
received guided wave (Sha and Lissenden 2021). The ferromag-
netic material’s mechanical stress and the magnetic field have
a nonlinear effect on magnetostriction. However, if the mate-
rial’s response consists of minor deviations around an operat-
ing point (bias point), the effect can be modeled using linear
coupled constitutive equations in either a stress-magnetization
or a strain-magnetization form, as described by the following
equations (COMSOL 2023 Sha and Lissenden 2021).
Stress-magnetization relationship: ​ ​
(3)​ σ =​ c​H​​ ε − ​ e​HS​​ T H​ ​ ​
(4)​ B =​ e​HS​​ ε +​ μ​0​​ ​ μ​rS​​ H​
Strain-magnetization relationship: ​ ​
(5)​ ε =​ s​H​​ σ +​ dHT​​ ​ T H​ ​ ​
(6)​ B =​ dHT​​ ​ σ +​ μ​0​​ ​ μ​rT​​ H​
where​
σ​ is the stress,
ε is the strain,
H is the magnetic field vector,
B is the magnetic flux density vector,
µ0 is the magnetic permeability of free space,
cH and sH are the stiffness and compliance matrices
measured at the constant magnetic field, respectively,
μrS and μrT are the relative magnetic permeabilities
measured at constant strain and stress, respectively, and
the matrices dHT and eHS are called piezomagnetic coupling
matrices.
As the applied magnetic field increases in intensity, the mag-
netostrictive strain on the material also increases. Ferromagnetic
materials that are isotropic and have few impurities are the most
effective in magnetostriction because these properties allow the
molecular dipoles of the materials to rotate easily. In a typical
ferromagnetic material, the relationship between the applied
magnetic field H and the relative change in length (that is, strain
[ε =∆L/L]) is highly nonlinear (Kim and Kwon 2015).
ME
|
RAILROADS
e
H
H =0
L =Fractional change
H =0
H
ΔL ΔL
Figure 2.
Magnetostriction
phenomena in
ferromagnetic materials:
(a) magnetic domains
alignment under the
external magnetic
field (b) change in the
length due to change in
magnetization.
44
M A T E R I A L S E V A L U A T I O N • J A N U A R Y 2 0 2 4
2401 ME January.indd 44 12/20/23 8:01 AM

Initial Experimental Trials
There is a significant history of trying to use surface waves
for the inspection of railroad wheels dating back to the late
1980s (Schramm et al. 1988, 1989). The first known tests were
conducted using piezoelectric transducers under a rubber
boot filled with liquid, but this combination proved too fragile
for practical use. In the late 2000s, other researchers also tried
using surface waves generated with EMAT sensors with some
improvements (Fan and Jia 2008 Salzburger et al. 2009).
However, whether generated with piezoelectric transducers or
EMATs, surface waves have important limitations associated
with particle motion and wave penetration. Surface waves follow
an elliptical pattern with both horizontal and vertical out-of-
plane motions, which make the waves highly susceptible to the
surface conditions of the structure where the waves propagate.
Water, dirt, rust, or contaminants on the wheel’s surface can
scatter and attenuate the wave, thereby reducing the range and
ability of the EMAT sensor and technique to find defects.
The first EMAT technique researched and explored for the
in-motion inspection of railcar wheels involved using bulk waves
(0°). These tests were designed to determine whether EMATs
could replace the existing in-track ultrasonic system previously
evaluated by MxV Rail. For these tests, the wheelset rotated on
casters, as shown in Figure 3, and the rotating wheelset was
tested using a sensor mounted on a table next to each wheel
on the wheelset. The sensor fired continuously as the wheel
rotated. The custom sensor included a spring-loaded fixture that
engaged and disengaged the wheel and an eight-channel EMAT
RF coil that generates shear waves at 0° from the point of entry
(normal beam). The shear sensors were selected because the
EMAT generates longitudinal waves (L-waves) on ferromagnetic
materials inefficiently (Zhang et al. 2022).
After testing several wheelsets with natural and manufac-
tured flaws, researchers found that the EMAT shear sensors
could detect all the defects on the wheel, but the results were
heavily affected by the cold-worked layer close to the wheel
tread. This cold-worked area did not affect the L-waves gen-
erated with piezoelectric transducers but did reflect normal
beam shear energy. Figure 4 shows the C-scan image for a
calibration wheel with various diameter flat-bottom holes
Figure 3. (a) wheelset fixture (b) custom EMAT sensors.
FBH–1/2 in. dia.
FBH–1/4 in. dia.
0
0.031
0.030
0.025
0.020
0.015
0.010
0.005
0.000
20 40 60
Distance (in.)
80 100 109.25
CAL–wheel
left side
FBH–1 in. dia.
Figure 4. Detection
of real defects on top
(inside of wheel) and
reflections from cold-
worked area on bottom.
J A N U A R Y 2 0 2 4 • M A T E R I A L S E V A L U A T I O N 45
2401 ME January.indd 45 12/20/23 8:01 AM
Distance
(in.)