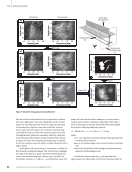
the design criteria with the Fine Tree suffering more with the
outliers as expressed by the larger variance compared to the
Wide ANN.
Tables 3 and 4 present the findings using the reduced
feature sets found in the Feature Extraction and RNT
Prediction section. The model with the smallest MAE is
emphasized in bold. With filtering down to 30 frequencies
instead of 700, the GPR and SVM were able to successfully
converge while the GPR surpasses the performance of the
ANNs. Using mRMR, the exponential GPR achieves an MAE
ME
|
RAILROADS
T A B L E 3
Machine learning algorithm sweep results for stress (MPa) using top 30 mRMR features
Model Type Mean absolute error Mean-squared error R2
Linear Linear 3.611 17.83 0.940
Linear Interactions 3.346 15.86 0.946
Linear Robust 3.542 17.95 0.939
Tree Fine 3.346 15.86 0.946
Tree Medium 2.624 17.10 0.942
Tree Coarse 2.701 16.77 0.943
SVM Linear 2.716 15.23 0.948
SVM Quadratic 3.606 18.07 0.939
SVM Cubic 2.946 12.85 0.957
SVM Fine Gaussian 2.781 11.43 0.961
SVM Medium Gaussian 2.230 9.11 0.969
SVM Coarse Gaussian 2.463 9.47 0.968
Ensemble Boosted trees 2.872 12.00 0.959
Ensemble Bagged trees 2.846 12.33 0.958
GPR Rational quadratic 2.512 13.58 0.954
GPR Squared exponential 2.544 9.996 0.966
GPR Matern 5/2 2.176 8.196 0.972
GPR Exponential 1.776 6.749 0.977
ANN Narrow 1.973 7.412 0.975
ANN Medium 2.553 10.35 0.965
ANN Wide 2.397 9.306 0.969
ANN Bilayered 2.146 8.153 0.972
ANN Trilayered 2.391 9.361 0.968
Kernel SVM kernel 2.338 9.229 0.969
Kernel Least-squares kernel 3.402 16.15 0.945
Note: Best is shown in red
0
0
5
10
15
–2 –4 –6 2 4
MAE: 1.08
MSE: 1.74
6
RNT error (°C)
0
0
5
10
15
–2 –4 –6 2 4
MAE: 1.41
MSE: 3.26
6
RNT error (°C)
Figure 10. Histogram of RNT
errors using predicted stresses
using all features: (a) Wide
ANN and (b) Fine Tree, one of
the worst-performing models.
The Wide ANN manages to
restrain much of the predictions
within the desired 2.78 °C
criteria, while the Fine Tree
suffers.
76
M A T E R I A L S E V A L U A T I O N • J A N U A R Y 2 0 2 4
2401 ME January.indd 76 12/20/23 8:01 AM
Number
of
observations
×
105
Number
of
observations
×
105

and MSE of 1.78 and 6.75 MPa, which are very close to the
ANN performance using 700 features. Converting to RNT,
these errors come out to 0.75 and 1.20 °C, respectively. On the
NCA side, the same GPR performs slightly better by 0.2 MAE
and 1 MSE, demonstrating the NCA’s slight edge over mRMR.
However, given the small degree of error, both methods could
be used interchangeably and this validates the use of feature
extraction for the previous methods proposed by the authors.
Conclusions
This paper presented the latest results relative to a vibration-
based NDT method, currently under development at the
University of Pittsburgh, to determine longitudinal stress and
neutral temperature in continuous welded rail. Specifically, the
study presented in this paper aimed at determining the most
significant bandwidths of interest that could be used to train
an ML algorithm to achieve the scope of the testing approach.
In addition, a systematic cross comparison of the predictions
from seven different ML algorithms was conducted.
The results demonstrated that only a few selected band-
widths within the frequency range of 0–700 Hz can be used
without compromising the accuracy of the proposed method-
ology. In addition, the Gaussian process regression and ANNs
outperformed the others. The analyses conducted here were
based on a relatively small set of experimental data collected
during four days of testing. Once fully proven, the method will
require only a few measurements to be taken at any time of the
day, regardless of the steel temperature.
As the current approach relies on knowing the neutral
temperature associated with the empirical data used for the
T A B L E 4
Machine learning algorithm sweep results for stress (MPa) using top 30 NCA features
Model Type Mean absolute error Mean-squared error R2
Linear Linear 3.607 17.76 0.940
Linear Interactions 3.197 14.73 0.950
Linear Robust 3.535 17.83 0.940
Tree Fine 3.201 14.73 0.950
Tree Medium 2.358 14.84 0.950
Tree Coarse 2.390 13.95 0.953
SVM Linear 2.386 12.55 0.958
SVM Quadratic 3.630 18.01 0.939
SVM Cubic 2.722 11.50 0.961
SVM Fine Gaussian 2.581 10.19 0.966
SVM Medium Gaussian 2.017 7.792 0.974
SVM Coarse Gaussian 2.272 8.365 0.972
Ensemble Boosted trees 2.662 10.80 0.963
Ensemble Bagged trees 2.753 11.52 0.961
GPR Rational quadratic 2.205 11.58 0.961
GPR Squared exponential 2.213 8.275 0.972
GPR Matern 5/2 1.857 6.730 0.977
GPR Exponential 1.527 5.678 0.981
ANN Narrow 1.657 5.981 0.980
ANN Medium 2.397 9.302 0.969
ANN Wide 2.211 8.385 0.972
ANN Bilayered 1.922 7.211 0.976
ANN Trilayered 2.182 8.265 0.972
Kernel SVM kernel 2.078 8.133 0.972
Kernel Least-squares kernel 3.599 21.69 0.927
Note: Best is shown in red
J A N U A R Y 2 0 2 4 • M A T E R I A L S E V A L U A T I O N 77
2401 ME January.indd 77 12/20/23 8:01 AM