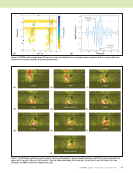
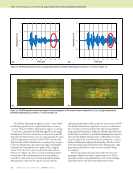
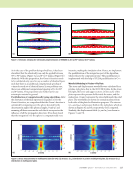
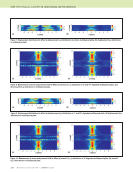
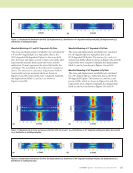
116 M A T E R I A L S E V A L U A T I O N • J A N U A R Y 2 0 2 0 Comparison of Wavefields in 4-Ply Pristine and Degraded Plate Along a Line Looking at Figures 6 through 13 in the wavefield, it is hard to distinguish if the 5% void material state degradation has at all contributed to change the magnitude of the wavefield, which may cause a perturbation to the NDE ultrasonic signals. To investigate further, the wavefield is plotted along a central line shown in Figure 14a. The plot is compared between the pristine, 0° degraded, 90° degraded, and 0° and 90° degraded plate as shown in Figure 14b. Discussion A (90/0)2 multilayered composite material is considered where the 90° lamina is transversely isotropic with the fiber direction along the y direction, and the 0° lamina is trans- versely isotropic with the fiber direction along the x direction. It is known that the wave energy tends to propagate along the fiber direction in transversely isotropic media. From the observation of stress and displacement fields, we can see that the wave is propagating along the length of the plate in the 0° plies with higher amplitude. We also observe that the wave decay in the 0° plies is faster than in the 90° plies. It is because the fiber direction is orthogonal to the wave propagation direction. In general, the wave decays farther away from the transducer location as the wave travels farther away from the point of impact of the ultrasonic beam. In regard to the effect of the material degradation, it can be seen that there is a slight reduction in the amplitude of the wavefields in the layers where the voids are introduced, as shown in Figures 8 through 13. Cases where the voids were introduced in both 0° and 90° (Figures 8 and 9), amplitude reduction in the wavefields are observed in both layers. Whereas, in cases where the voids were introduced in either the 0° (Figures 10 and 11) or 90° (Figures 12 and 13) layers, maximum effect was in the respective layer, but overall ampli- tudes of the wavefield in the 4-ply system also decreased. The phenomena are more distinctly observed in a line plot of the wave amplitude along the central line shown in Figure 14b. It is even more relevant when compared with the pristine layers. The simulation has been conducted under the same conditions for all the lamina. However, the effect of the presence of the void (the amplitude reduction) is much more distinctly observed in the degraded layers. It can be seen that the amplitude is lower at the 90° layer when the 90° layer is degraded compared to the pristine amplitude. Similarly, the amplitude is lower at the 0° layer zone when the 0° layer is degraded. And the amplitude is lower at both zones when both the 0° and 90° layer are degraded. However, such a distinct phenomenon can’t be observed in the pristine, although a slight effect is visible due to the impact of the degraded layers. It can be clearly observed and concluded that the ultra- sonic field changes with the presence of internal damages and discontinuities as it changes the effective material properties. Due to the damage, the effective material property or stiffness degrades. Thus, when the wave interacts with the damages (a degraded layer), it loses its energy, resulting in a reduction in amplitude of wavefield. Therefore, it can be concluded that the damages and discontinuities present in microscale can affect the wavefield and can also possibly affect the ultrasonic ME TECHNICAL PAPER w computational nde for composites R S A R A S A 3* A 5* A 1 A 4 C E D Solid Fluid 1 Fluid 2 0 5 6 7 8 1 2 3 4 5 Z axis (mm) Pristine 90° degraded 0° degraded Both degraded 0° layer 90° layer 0° layer 90° layer Figure 14. The experimental NDE problem shown as: (a) cross-sectional view along the x-z plane showcasing the central line where the wave amplitude is plotted (b) line plot of wave amplitude along the central line. (a) (b) Wave amplitude

J A N U A R Y 2 0 2 0 • M A T E R I A L S E V A L U A T I O N 117 signal (which is not shown in this paper). Effect of the degraded material properties due to microscale damage is successfully incorporated in the CNDE models. Conclusion In this paper, the effect of a microscale discontinuity, such as a void, in the material state is presented. A new CNDE tech- nique, the distributed point source method (DPSM), was used to simulate a wavefield in both a pristine and degraded multilayered anisotropic solid plate. The generalized anisotropic displacement and the stress Green’s function were developed, followed by SISMAG and parallelization to increase the computational efficiency. The change in the macroscale constitutive matrix due to the presence of voids was calculated. The algorithms were implemented in a CUDA-enabled C++ programming environment. DPSM was used to model the superposition of an ultrasonic pulse-echo and through-transmission NDE technique. The wavefield generated by a finite size transducer near a fluid–solid inter- face and the stress fields inside both the fluid and solid media were computed for normal incidence. Wavefields in pristine and degraded 4-ply anisotropic plate were compared, and the change in ultrasonic field due to damage was verified. ACKNOWLEDGEMENT The author would like to acknowledge NASA Langley Research Center (LaRC) for funding the research under Contract no. NNL15AA16C. The authors would like to thank Professor J.D. Achenbach for valuable discus- sions on Green’s function during 2015. REFERENCES Bakhvalov, N.S., and G. Panasenko, 1989, Homogenisation: Averaging Processes in Periodic Media: Mathematical Problems in the Mechanics of Composite Materials, Springer, New York, NY. Ballisti, R., and C. Hafner, 1983, “The Multiple Multipole Method (MMP) in Electro and Magnetostatic Problems,” IEEE Transactions on Magnetics, Vol. 19 No. 6, pp. 2367–2370. Banerjee, S., and S. Shrestha, 2018, “Numerical Modeling of Ultrasonic Wave Propagation in Composites,” Computational and Experimental Methods in Structures: Structural Health Monitoring for Advanced Composite Structures, Vol. 8, pp. 93–124. Banerjee, S., and T. Kundu, 2006a, “Symmetric and Anti-Symmetric Rayleigh-Lamb Modes in Sinusoidally Corrugated Waveguides: An Analyt- ical Approach,” International Journal of Solids and Structures, Vol. 43, No. 21, pp. 6551–6567. Banerjee, S., and T. Kundu, 2006b, “Elastic Wave Propagation in Sinu- soidally Corrugated Waveguides,” The Journal of the Acoustical Society of America, Vol. 119, No. 4, pp. 2006–2017. Banerjee, S., and T. Kundu, 2007b, “Advanced Application of Distributed Point Source Method - Ultrasonic Field Modeling in Solid media,” in DPSM for Modeling Engineering Problems, John Wiley & Sons, Hoboken, New Jersey, Ch. 4. Banerjee, S., and T. Kundu, 2007a, “Ultrasonic Field Modeling in Plates Immersed in Fluids,” International Journal of Solids and Structures, Vol. 44, No. 18–19, pp. 6013–6029. Banerjee, S., and T. Kundu, 2008a, “Semi-Analytical Modeling of Ultra- sonic Fields in Solids with Internal Anomalies Immersed in a Fluid,” Wave Motion, Vol. 45, No. 5, pp. 581–595. Banerjee, S., and T. Kundu, 2008b, “Elastic Wave Field Computation in Multilayered Nonplanar Solid Structures: A Mesh-Free Semianalytical Approach,” The Journal of Acoustical Society of America, Vol. 123, No. 3, pp. 1371–1382. Banerjee, S., S. Das, T. Kundu, and D. Placko, 2009, “Controlled Space Radiation Concept for Mesh-Free Semi-Analytical Technique to Model Wave Fields in Complex Geometries,” Ultrasonics, Vol. 48, No. 8, pp. 615–622. Banerjee, S., T. Kundu, and N.A. Alnuaimi, 2007, “DPSM Technique for Ultrasonic Field Modelling Near Fluid-Solid Interface,” Ultrasonics, Vol. 46, No. 3, pp. 235–250. Berger, H., S. Kari, U. Gabbert, R. Rodriguez-Ramos, R. Guinovart, J.A. Otero, and J. Bravo-Castillero, 2005, “An Analytical and Numerical Approach for Calculating Effective Material Coefficients of Piezoelectric Fiber Composites,” International Journal of Solids and Structures, Vol. 42, No. 21–22, pp. 5692–5714. Bouchon, M., and F.J. Sánchez-Sesma, 2007, “Boundary Integral Equations and Boundary Elements Methods in Elastodynamics,” Advances in Geophysics, Vol. 48, pp. 157–189. Burridge, R., 1971, “Lamb’s Problem for an Anisotropic Half-Space,” The Quarterly Journal of Mechanics and Applied Mathematics, Vol. 24, No. 1, pp. 81–98. Every, A.G., and K.Y. Kim, 1996, “Determination of Elastic Constants of Anisotropic Solids from Elastodynamic Green’s Functions,” Ultrasonics, Vol. 34, No. 2–5, pp. 471–472. Glushkov, E., N. Glushkova, and A. Eremin, 2011, “Forced Wave Propaga- tion and Energy Distribution in Anisotropic Laminate Composites,” The Journal of the Acoustical Society of America, Vol. 129, No. 5, pp. 2923–2934. Hafner, C., 1985, “MMP Calculations of Guided Waves,” IEEE Transac- tions on Magnetics, Vol. 21, No. 6, pp. 2310–2312. Imhof, M.G., 2004, “Computing the Elastic Scattering from Inclusions Using the Multiple Multipoles Method in Three Dimensions,” Geophysical Journal International, Vol. 156, No. 2, pp. 287–296. Kraut, E.A., 1963, “Advances in the Theory of Anisotropic Elastic Wave Propagation,” Reviews of Geophysics, Vol. 1, No. 3, pp. 401–448. Krowne, C.M., 1984, “Fourier Transformed Matrix Method of Finding Propagation Characteristics of Complex Anisotropic Layered Media,” IEEE Transactions on Microwave Theory and Techniques, Vol. 32, No. 12, pp. 1617–1625. Leckey, C.A.C., M.D. Rogge, and F.R. Parker, 2014, “Guided Waves in Anisotropic and Quasi-Isotropic Aerospace Composites: Three- Dimensional Simulation and Experiment,” Ultrasonics, Vol. 54, No. 1, pp. 385–394. Lenglet, E., A.-C. Hladky-Hennion, and J.-C. Debus, 2003, “Numerical Homogenization Techniques Applied to Piezoelectric Composites,” The Journal of the Acoustical Society of America, Vol. 113, No. 2, pp. 826–833. Medeiros, R. de, M.E. Moreno, F.D. Marques, and V. Tita, 2012, “Effective Properties Evaluation for Smart Composite Materials,” Journal of the Brazilian Society of Mechanical Sciences and Engineering, Vol. 34, no. spe, pp. 362–370. Michalski, K.A., and J.R. Mosig, 1997, “Multilayered Media Green’s Func- tions in Integral Equation Formulations,” IEEE Transactions on Antennas and Propagation, Vol. 45, No. 3, pp. 508–519. Moll, J., C. Rezk-Salama, R.T. Schulte, T. Klinkert, C.-P. Fritzen, and A. Kolb, 2011, “Interactive Simulation and Visualization of Lamb Wave Prop- agation in Isotropic and Anisotropic Structures,” Journal of Physics: Confer- ence Series, Vol. 305, No.1, doi: 10.1088/1742-6596/305/1/012095. Moreno, M.E., V. Tita, and F.D. Marques, 2009, “Finite Element Analysis Applied to Evaluation of Effective Material Coefficients for Piezoelectric Fiber Composites,” Brazilian Symposium on Aerospace Engineering & Applications, São Paulo, Brazil. Newberry, B.P., and R.B. Thompson, 1989, “A Paraxial Theory for the Propagation of Ultrasonic Beams in Anisotropic Solids,” The Journal of the Acoustical Society of America, Vol. 85, No. 6, pp. 2290–2300.