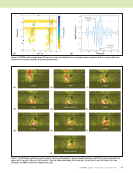
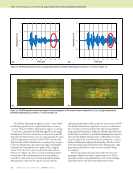
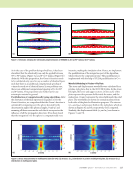
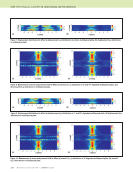
118 M A T E R I A L S E V A L U A T I O N • J A N U A R Y 2 0 2 0 Payton, R.C., 1983, Elastic Wave Propagation in Transversely Isotropic Media, Martinus Nijhoff Publishers, Hague, Netherlands, Vol. 4. Placko, D. and T. Kundu, 2001, “Theoretical Study of Magnetic and Ultra- sonic Sensors: Dependence of Magnetic Potential and Acoustic Pressure on the Sensor Geometry,” 6th Annual International Symposium on NDE for Health Monitoring and Diagnostics, Newport Beach, California. Placko, D., and T. Kundu, 2007, DPSM for Modeling Engineering Problems, John Wiley & Sons, Hoboken, NJ. Placko, D., T. Kundu, and R. Ahmad, 2002, “Theoretical Computation of Acoustic Pressure Generated by Ultrasonic Sensors in the Presence of an Interface,” NDE for Health Monitoring and Diagnostics, San Diego, CA. Pointer, T., E. Liu, and J.A. Hudson, 1998, “Numerical Modelling of Seismic Waves Scattered by Hydrofractures: Application of the Indirect Boundary Element Method,” Geophysical Journal International, Vol. 135, No. 1, pp. 289–03. Qin, R.-S., Y. Xiao, and H. Lan, 2014, “Numerical Simulation of Effective Properties of 3D Piezoelectric Composites,” Journal of Engineering, Vol. 2014, Article ID: 824806. Rahani, E.K., and T. Kundu, 2011, “Gaussian-DPSM (G-DPSM) and Element Source Method (ESM) Modifications to DPSM for Ultrasonic Field Modeling,” Ultrasonics, Vol. 51, No. 5, pp. 625–631. Rajamohan, C., and J. Raamachandran, 1999, “Bending of Anisotropic Plates by Charge Simulation Method,” Advances in Engineering Software, Vol. 30, No. 5, pp. 369–373. Sánchez-Sesma, F.J., and M. Campillo, 1991, “Diffraction of P, SV and Rayleigh Waves by Topographic Features: A Boundary Integral Formula- tion,” Bulletin of the Seismological Society of America, Vol. 81, No. 6, pp. 2234–2253. Sánchez-Sesma, F.J., and M. Campillo, 1993, “Topographic Effects for Incident P, SV and Rayleigh Waves,” Tectonophysics, Vol. 218, No 1–3, pp. 113–125. Shaw, R.P., 1979, “Boundary Integral Equation Methods Applied to Wave Problems,” in Developments in Boundary Element Methods, edited by P.K. Banerjee and R. Butterfield, Applied Science Publishers, London, England, pp. 121–153. Shrestha, S., 2017, “Computational Wave Field Modeling using Sequential Mapping of Poly-Crepitus Green’s Function in Anisotropic Media,” (Doctoral Dissertation), https://scholarcommons.sc.edu/etd/4419/. Shrestha, S., and S. Banerjee, 2016, “DPSM Modeling of Wave Propagation in Anisotropic Half Space,” American Society for Composites: Thirty-First Technical Conference, Williamsburg, VA. Shrestha, S., and S. Banerjee, 2017, “Computational Wave Field Modeling in Anisotropic Plate,” SPIE Smart Structures and Materials + Nondestruc- tive Evaluation and Health Monitoring, Portland, OR. Shrestha, S., and S. Banerjee, 2018, “Virtual Nondestructive Evaluation for Anisotropic Plates Using Symmetry Informed Sequential Mapping of Anisotropic Green’s Function (SISMAG),” Ultrasonics, Vol. 88, pp. 51–63. Spies, M., 1999, “Transducer Field Modeling in Anisotropic Media by Superposition of Gaussian Base Functions,” The Journal of the Acoustical Society of America, Vol. 105, No. 2, pp. 633–638. Sun, C.T., and R.S. Vaidya, 1996, “Prediction of Composite Properties from a Representative Volume Element,” Composites Science and Tech- nology, Vol. 56, No. 2, pp. 171–179. Swaminathan, S., and S. Ghosh, 2006, “Statistically Equivalent Representa- tive Volume Elements for Unidirectional Composite Microstructures: Part II-with Interfacial Debonding,” Journal of Composite Materials, Vol. 40, No. 7, pp. 605–621. Swaminathan, S., S. Ghosh, and N.J. Pagano, 2006, “Statistically Equivalent Representative Volume Elements for Unidirectional Composite Microstructures: Part I-Without damage,” Journal of Composite Materials, Vol. 40, No. 7, pp. 583–604. Tavaf, V., M. Saadatzi, and S. Banerjee, 2019, “Quantification of Degraded Constitutive Coefficients of Composites in the Presence of Distributed Defects,” Journal of Composite Materials, Vol. 53, No. 18, pp. 2517–2529. Tavaf, V., M. Saadatzi, S. Shrestha, and S. Banerjee, 2018a, “Effect of Multi- scale Precursor Damage on Wave Propagation through Modulated Consti- tutive Properties of Composite Materials,” SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Denver, CO. Tavaf, V., M. Saadatzi, S. Shrestha, and S. Banerjee, 2018b, “Quantification of Material Degradation and its Behavior of Elastodynamic Green’s Function for Computational Wave Field Modeling in Composites,” Mate- rials Today Communications, Vol. 17, pp. 402–412. Wada, Y., T. Kundu, and K. Nakamura, 2014, “Mesh-Free Distributed Point Source Method for Modeling Viscous Fluid Motion Between Disks Vibrating at Ultrasonic Frequency,” The Journal of the Acoustical Society of America, Vol. 136, No. 2, pp. 466–474. Wang, C.-Y., and J.D. Achenbach, 1992, “A New Look at 2-D Time- Domain Elastodynamic Green’s Functions for General Anisotropic Solids,” Wave Motion, Vol. 16, No. 4, pp. 389–405. Wang, C.-Y., and J.D. Achenbach, 1993, “A New Method to Obtain 3-D Green’s Functions for Anisotropic Solids,” Wave Motion, Vol. 18, No. 3, pp. 273–289. Weilinger Associates, 2009, “Finite Element Analysis of Propagating Elastic Waves” (report based on software package), Weilinger Associates Inc., New York, NY. Wen, J.J., and M.A. Breazeale, 1988, “A Diffraction Beam Field Expressed as the Superposition of Gaussian Beams,” Journal of the Acoustical Society of America, Vol. 83, No. 5, pp. 1752–1756. Willis, J., 1991, “Inclusions and Cracks in Constrained Anisotropic Media,” Modern Theory of Anisotropic Elasticity and Applications, pp. 87–102. Willis, J.R., 1973, “Self-Similar Problems in Elastodynamics,” Philosophical Transactions of the Royal Society of London, Series A, Mathematical, Physical and Engineering Sciences, Vol. 274, No. 1240, pp. 435–491. Yeatts, F.R., 1984, “Elastic Radiation from a Point Force in an Anisotropic Medium,” Physical Review B, Vol. 29, No. 4, pp. 1674–1684. Zhao, X., and Rose, J.L., 2003, “Boundary Element Modeling for Defect Characterization Potential in a Wave Guide,” International Journal of Solids and Structures, Vol. 40, No. 11, pp. 2645–2658. ME TECHNICAL PAPER w computational nde for composites

J A N U A R Y 2 0 2 0 • M A T E R I A L S E V A L U A T I O N 119 SERVICE directory EMPLOYMENT SERVICE Looking for a job or an employee? Email Assistant Editor Cara Schaurer at cschaurer@asnt.org for information on listing your qualifications in Materials Evaluation. This is a free service for ASNT members. Our Employment Service listings can also be found in the NDT Jobs section of ASNT’s website at asnt.org. ASNT is not responsible for the authen- ticity or accuracy of the information herein. Candidates do not carry the endorsement or recommendation of ASNT.